« 今年はじめての積雪 | 最新記事 | 雛人形を飾りました »
2015年1月30日
アルゴリズムって大事
センター試験も終わり、これから本格的な入試の時期に入ります。
受験生の皆さんは、インフルエンザに注意して、実力を出し切ってください。
今日のブログはちょっとコーヒーブレイク的な内容です。
問題‥下図のような道路︵黒い線︶がある。Ａ地点からＢ地点まで行く経路は何通りあるか。 ただし、同じ道を2回通らないこと。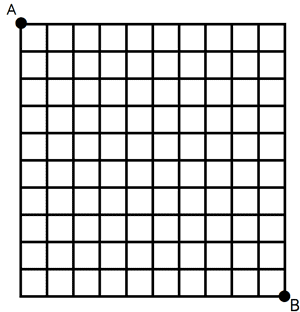
一見、簡単そうな問題ですね。
上図は10×10の区画に区切られた道路ですが、１×１、２×２...の場合で考えてみて一般化していけば解けるかな？ そうなると順列組合わせで、答えは 20C10 = (20×19×18×17×16×15×14×13×12×11)/(10×9×8×7×6×5×4×3×2✕1) = 184,756 通りかな？ ・・・・・ しかし、そう簡単ではありません。 最短経路だけとは限らないですから。 日本科学未来館の作製した動画が面白いので、こちらをごらんください。 この動画に、上の問題の答えが掲載されています。親切ですね~
﹃フカシギの数え方﹄ おねえさんといっしょ！ みんなで数えてみよう！ ︵日本科学未来館公式︶ このように、何通りあるかを逐一辿って検証してみると、一見簡単に解答が得られそうに見えて、とんでもないことになるのです。 そこで必要なことが﹁アルゴリズム﹂の最適化です。 アルゴリズムとは、解答に至るための具体的な手順のことをいいます。
動画にあるように、シラミつぶし的に全ての経路を検証する方法は方法論としては単純ですが、効率の面では非効率きわまりありません。 そして、コンピューターはいくら性能が良くても、今のコンピューターは残念ながら﹁考える力﹂を持ち合わせていません。 人間の命令に従った計算を行ない、その結果を出しているだけです。 したがって、解答に至るまでの最適化した手順を併せてコンピューターに教えてあげないと、計算にとても時間がかかってしまうのです。 いかに正しく効率的なアルゴリズムを提示できるか、これが重要なのです。 →関連ブログ記事 一番じゃなくても一番になれる エレガントに解くということ ということで、上の問題を適切なアルゴリズムで計算すると、スーパーコンピューターで何万年もかかるものが、パソコンでも数秒で解答が得られる、という事例が下記の動画です。 これもアルゴリズムの一例であり、もちろん、さらに正しく効率的なアルゴリズムも存在することでしょう。
身近なところではカーナビの経路とか、乗換案内のルート検索とか、様々な場面で応用されています。 数学は奥が深いですね。 それにしても組合せ爆発・・・・オソロシス・・・・・
そういえば、ザ・ぼんち︵おさむ、まさと︶のギャグで﹁A地点からB地点まで 行くあいだに既に恋をしてたんです﹂ってのがありました。
つい思い出してしまいました。古い！
■関連ブログ記事
一番じゃなくても一番になれる
エレガントに解くということ
友達の友達は皆友達だ か？
お寺の屋根が曲線である理由・別の視点から
お寺の屋根が美しいのには理由があります
一義的に求められない数値もある
IPアドレス枯渇解消へ
問題‥下図のような道路︵黒い線︶がある。Ａ地点からＢ地点まで行く経路は何通りあるか。 ただし、同じ道を2回通らないこと。
一見、簡単そうな問題ですね。
上図は10×10の区画に区切られた道路ですが、１×１、２×２...の場合で考えてみて一般化していけば解けるかな？ そうなると順列組合わせで、答えは 20C10 = (20×19×18×17×16×15×14×13×12×11)/(10×9×8×7×6×5×4×3×2✕1) = 184,756 通りかな？ ・・・・・ しかし、そう簡単ではありません。 最短経路だけとは限らないですから。 日本科学未来館の作製した動画が面白いので、こちらをごらんください。 この動画に、上の問題の答えが掲載されています。親切ですね~
﹃フカシギの数え方﹄ おねえさんといっしょ！ みんなで数えてみよう！ ︵日本科学未来館公式︶ このように、何通りあるかを逐一辿って検証してみると、一見簡単に解答が得られそうに見えて、とんでもないことになるのです。 そこで必要なことが﹁アルゴリズム﹂の最適化です。 アルゴリズムとは、解答に至るための具体的な手順のことをいいます。
動画にあるように、シラミつぶし的に全ての経路を検証する方法は方法論としては単純ですが、効率の面では非効率きわまりありません。 そして、コンピューターはいくら性能が良くても、今のコンピューターは残念ながら﹁考える力﹂を持ち合わせていません。 人間の命令に従った計算を行ない、その結果を出しているだけです。 したがって、解答に至るまでの最適化した手順を併せてコンピューターに教えてあげないと、計算にとても時間がかかってしまうのです。 いかに正しく効率的なアルゴリズムを提示できるか、これが重要なのです。 →関連ブログ記事 一番じゃなくても一番になれる エレガントに解くということ ということで、上の問題を適切なアルゴリズムで計算すると、スーパーコンピューターで何万年もかかるものが、パソコンでも数秒で解答が得られる、という事例が下記の動画です。 これもアルゴリズムの一例であり、もちろん、さらに正しく効率的なアルゴリズムも存在することでしょう。
身近なところではカーナビの経路とか、乗換案内のルート検索とか、様々な場面で応用されています。 数学は奥が深いですね。 それにしても組合せ爆発・・・・オソロシス・・・・・
投稿者: kameno 日時: 2015年1月30日 21:17