« 私のお墓の前で泣かないでください | 最新記事 | 生体活動のもつカオス的揺らぎ »
2007年1月10日
毫釐も差あれば天地懸に隔たり
毫釐も差あれば、天地懸に隔たり
︵ごうりもさあれば てんちはるかにへだたり︶
道元禅師により著された﹃普勧坐禅儀﹄の一節です。
三祖大師﹃信心銘﹄にも﹁毫釐も差あれば、天地懸かに隔たる。現前を得んと欲せば、順逆を存すること莫れ﹂とありますが、漢和辞典を紐解くと、 毫は、ごく少し。わずか。蚕の口から出る糸十本。 釐は、分の十分の一。極めて小さい数量。 とあります。 豪釐の用例として、漢和辞典には﹃漢書﹄巻六十二 司馬遷傳や﹃史記﹄太史公自序に﹁差以豪釐、謬以千里﹂という表現がありますので、中国ではかなり前から用いられた概念であることがわかります。 意味は、平たく言えば ﹁初めはごくわずかのちがいでも、終わりには大きなちがいになる﹂
ということですが、これは、科学、工学で最近用いられるカオス論理に通じるところがあります。 つまり、﹁毫釐も差あれば、天地懸かに隔たる﹂は、科学的に言えば、﹁初期状態への敏感な依存性﹂という言葉で言い表されます。 この﹁初期状態への敏感な依存性﹂というのは、すなわち、カオスの特徴を表わす言葉に他ならないのです。 カオスは、気象学者ローレンツが、気象の予測としてコンピュータで計算した出力結果が、初期値の僅かな違いによって結果が全く違ってしまうことに気づいたことにより見い出された概念です。
カオスを簡単に定義すると、 ﹁決定論的なシステムがつくり出す非周期振動﹂ と言うことができます。 これは、後ほど出てくるロジスティック写像の計算を実際に行ってみると、視覚的によくわかると思います。 決定論システム＝破ることができない不変の法則からなる系であり 非周期振動＝専ら偶然に支配される確率論的な運動という意味です。 また、カオスの特徴はといえば ︵1︶自己相似 ︵2︶単純な数式から、ランダムに見える複雑な振る舞いが発生する ︵3︶初期値のごくわずかなずれが、将来の結果に甚大な差を生み出す︵初期状態への敏感な依存性＝バタフライ効果︶ ︵4︶過去の観測データから将来の長期予測が困難となる wikiペディア ということが挙げられます。
なんだかよくわからない概念かもしれませんが・・・ 例えば、サイコロを50センチの高さから落とします。 落とす位置と角度を正確に測り、落とす床の面も精密に仕上げた状態で、1回目を落とします。 1から6の何らかの目が出るでしょう。 さて、2回目を、1回目の初期条件と全く同じように設定して、同じサイコロで、同一条件で落下させてみます。 ……それでも、きっと、結果は1回めとは違う目が出てしまうのではないでしょうか。 工業的には測定できない僅かな違いとか、たとえば空気の動き︵風のわずかな揺らぎ︶とか、地球の自転の加減とか、1回目で、サイコロにかすかな傷がついてしまったとか。 そんな程度の理由で、同じ目を︵偶然ではなく確実に︶出すことは不可能でしょう。
これが、﹁初期状態への敏感な依存性﹂ということなのです。 スタートの状態の僅かな違いが、結果としてまったく違って出てきてしまうのです。
カオスな系は、初期条件のわずかな差が時間とともに拡大して、結果に大きな違いをもたらす。そのことが﹁北京で蝶が羽ばたくと、ニューヨークで嵐が起こる﹂と、よく例えられ、これをバタフライ効果と呼んでいる。 Wikiペディア ということです。 もしかしたら、前述のサイコロの目の結果の違いは、地球の裏側の蝶の羽ばたきに拠るものも一因にあるかもしれませんね。
さて、このカオスを示す有名な計算式があります。 ロジスティック写像と呼ばれるものです。 例えば、連続時間の差分方程式として次のようなものを考えてみましょう。
x(t+1)=4x(t)(1-x(t)) という簡単な式です。 初期状態 t=0 のとき、初期値 x(0)を 0.2 とします。 すると、t=1 の時の x(ｔ) の値は x(1)=4x(0)(1-x(0)) =4×0.2×(1-0.2︶ =0.8×0.8 =0.64 ですね。 ︵t=2 以下も同様に計算︶
では、初期値 x(0)を 0.20000000000001 としてみましょう。 僅か 0.00000000000001 だけ違う、まさに﹁毫釐の差﹂です。 計算はエクセルで自動化できますので、ファイルで作ってみました。
エクセルファイル︵クリックしてダウンロード︶
結果をグラフに表すと・・・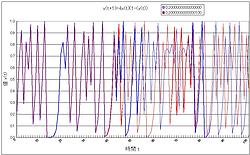
青い線が x(0) = 0.2
赤い線が x(0) = 0.20000000000001
の結果です。
t=40近辺までは、赤と青のグラフは、ほとんど重なって同じ挙動をします。
ところが、それを越えると、急に挙動が変わっていき、まるで全く別の計算式の結果を示しているかのようです。
これがカオスの﹁初期状態への敏感な依存性﹂を端的にしめしているわけですね。
こんな単純な計算式ですら複雑な挙動を示します。
事象の未来を予測することが、どれほどコンピューターが発達したとしても不可能であることがわかりますね。
毫釐も差あれば、天地懸に隔たり なかなか奥が深いです。 ︵以下続く︶
道元禅師により著された﹃普勧坐禅儀﹄の一節です。
三祖大師﹃信心銘﹄にも﹁毫釐も差あれば、天地懸かに隔たる。現前を得んと欲せば、順逆を存すること莫れ﹂とありますが、漢和辞典を紐解くと、 毫は、ごく少し。わずか。蚕の口から出る糸十本。 釐は、分の十分の一。極めて小さい数量。 とあります。 豪釐の用例として、漢和辞典には﹃漢書﹄巻六十二 司馬遷傳や﹃史記﹄太史公自序に﹁差以豪釐、謬以千里﹂という表現がありますので、中国ではかなり前から用いられた概念であることがわかります。 意味は、平たく言えば ﹁初めはごくわずかのちがいでも、終わりには大きなちがいになる﹂
ということですが、これは、科学、工学で最近用いられるカオス論理に通じるところがあります。 つまり、﹁毫釐も差あれば、天地懸かに隔たる﹂は、科学的に言えば、﹁初期状態への敏感な依存性﹂という言葉で言い表されます。 この﹁初期状態への敏感な依存性﹂というのは、すなわち、カオスの特徴を表わす言葉に他ならないのです。 カオスは、気象学者ローレンツが、気象の予測としてコンピュータで計算した出力結果が、初期値の僅かな違いによって結果が全く違ってしまうことに気づいたことにより見い出された概念です。
カオスを簡単に定義すると、 ﹁決定論的なシステムがつくり出す非周期振動﹂ と言うことができます。 これは、後ほど出てくるロジスティック写像の計算を実際に行ってみると、視覚的によくわかると思います。 決定論システム＝破ることができない不変の法則からなる系であり 非周期振動＝専ら偶然に支配される確率論的な運動という意味です。 また、カオスの特徴はといえば ︵1︶自己相似 ︵2︶単純な数式から、ランダムに見える複雑な振る舞いが発生する ︵3︶初期値のごくわずかなずれが、将来の結果に甚大な差を生み出す︵初期状態への敏感な依存性＝バタフライ効果︶ ︵4︶過去の観測データから将来の長期予測が困難となる wikiペディア ということが挙げられます。
なんだかよくわからない概念かもしれませんが・・・ 例えば、サイコロを50センチの高さから落とします。 落とす位置と角度を正確に測り、落とす床の面も精密に仕上げた状態で、1回目を落とします。 1から6の何らかの目が出るでしょう。 さて、2回目を、1回目の初期条件と全く同じように設定して、同じサイコロで、同一条件で落下させてみます。 ……それでも、きっと、結果は1回めとは違う目が出てしまうのではないでしょうか。 工業的には測定できない僅かな違いとか、たとえば空気の動き︵風のわずかな揺らぎ︶とか、地球の自転の加減とか、1回目で、サイコロにかすかな傷がついてしまったとか。 そんな程度の理由で、同じ目を︵偶然ではなく確実に︶出すことは不可能でしょう。
これが、﹁初期状態への敏感な依存性﹂ということなのです。 スタートの状態の僅かな違いが、結果としてまったく違って出てきてしまうのです。
カオスな系は、初期条件のわずかな差が時間とともに拡大して、結果に大きな違いをもたらす。そのことが﹁北京で蝶が羽ばたくと、ニューヨークで嵐が起こる﹂と、よく例えられ、これをバタフライ効果と呼んでいる。 Wikiペディア ということです。 もしかしたら、前述のサイコロの目の結果の違いは、地球の裏側の蝶の羽ばたきに拠るものも一因にあるかもしれませんね。
さて、このカオスを示す有名な計算式があります。 ロジスティック写像と呼ばれるものです。 例えば、連続時間の差分方程式として次のようなものを考えてみましょう。
x(t+1)=4x(t)(1-x(t)) という簡単な式です。 初期状態 t=0 のとき、初期値 x(0)を 0.2 とします。 すると、t=1 の時の x(ｔ) の値は x(1)=4x(0)(1-x(0)) =4×0.2×(1-0.2︶ =0.8×0.8 =0.64 ですね。 ︵t=2 以下も同様に計算︶
では、初期値 x(0)を 0.20000000000001 としてみましょう。 僅か 0.00000000000001 だけ違う、まさに﹁毫釐の差﹂です。 計算はエクセルで自動化できますので、ファイルで作ってみました。
エクセルファイル︵クリックしてダウンロード︶
結果をグラフに表すと・・・
青い線が x(0) = 0.2
赤い線が x(0) = 0.20000000000001
の結果です。
t=40近辺までは、赤と青のグラフは、ほとんど重なって同じ挙動をします。
ところが、それを越えると、急に挙動が変わっていき、まるで全く別の計算式の結果を示しているかのようです。
これがカオスの﹁初期状態への敏感な依存性﹂を端的にしめしているわけですね。
こんな単純な計算式ですら複雑な挙動を示します。
事象の未来を予測することが、どれほどコンピューターが発達したとしても不可能であることがわかりますね。
毫釐も差あれば、天地懸に隔たり なかなか奥が深いです。 ︵以下続く︶
投稿者: kameno 日時: 2007年1月10日 18:19
tenjin95さん
なるほど、老荘思想の渾沌もその一つでしょうか。
このあたりの源流を辿ると面白いかもしれないですね。
投稿者 kameno | 2007年1月10日 20:51