Teishoin's Digital Photo Log

昨日の記事の続きです。

一劫が何年かを計算してみましょう。

【計算上の定義】
芥子劫を１辺１由旬の城に芥子粒を満たし、100年ごとにそれを１粒づつ取り出して、芥子粒が空になるまでの時間とします。

【計算上の仮定】
１由旬の城を一辺が7km=7,000,000mmの立方体とします
また、芥子粒を直径0.5mmの球とします

（芥子の実。Wikipedia「ケシ」項より引用）

さて、一番単純な計算方法は、一つ一つの芥子粒がそれぞれ0.5mmの立方格子に入った状態で、この格子を角砂糖をジャングルジムのように積んでいくことを考えます。

すると、一辺には 14,000,000 個の芥子粒が並びますので、これを3乗して
2,744,000,000,000,000,000,000 個の芥子の実が詰ります。　
読み方は 27垓（がい）4400京（けい）個。

100年に１つづつこれを取り去るわけですから、全部取り去るまでには

274,400,000,000,000,000,000,000 年の歳月を要します。　
読み方は　2,744垓（がい）年。

ここまで計算したうえで、実際には芥子の実はさらに「きっちりと」詰まっていることが予測されます。
イメージとしては、八百屋の店先に積まれている蜜柑のような積み方です。

　
このことを考えたのがヨハネス・ケプラーです。
ケプラーは1611年、「物質を構成する粒子は体積を最小とするように自己を組織化するだろう」という構成原理に基づき、「六方最密充填」と「面心立方格子」が最高密度の配置であると予想しました。

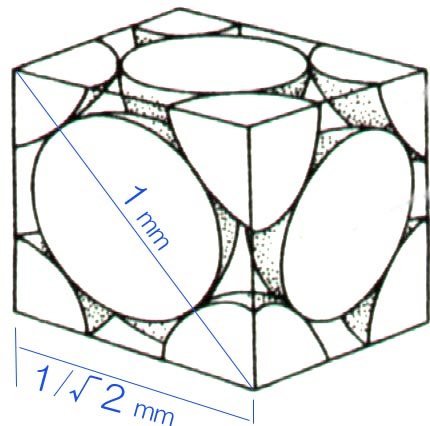
これが面心立方格子。こんな具合に詰まれている場合に最も充填率が高くなると予想しました。

このケプラーの予想は、実に約400年後の1998年、トマス・ヘールズによりコンピュータを使って虱潰しに精査するという手法により、ほぼ証明に至りました。

ということで、冒頭の単純に立体格子状に縦横に積んでい方法ですと、その充填率は球の体積の公式より　π/6 (＝ 52.3598･･･％)

六方最密充填、面心立方格子による充填率は、√2π/6 (＝ 74.08･･･%)

となりますので、芥子粒の数は　√2π/6 ÷　π/6 ＝ √2 倍増えます。

つまり、時間もそれに比例して増えますので、

一劫は274,400,000,000,000,000,000,000 ×　√2 ＝　388,000,000,000,000,000,000,000 年くらいだろうという計算結果となりました。

※ここまで適当に計算していますので、間違いあればご指摘ください

それにしても、このケプラー予想問題は、問題自体は単純でありますが、球を積むときにはどのように積むことが一番充填率が高いのか、未だ完全に証明されていないということが面白いですね。
もしかすると、面心立方格子よりももっと充填率の高いつめ方があるかもしれないのです。

これは人類の永遠の課題なのかも知れません。