Teishoin's Digital Photo Log

若田光一さんら7人の宇宙飛行士を乗せたスペースシャトル「ディスカバリー」の打上げが無事成功し、順調に飛行を続けています。
まずはおめでとうございます。

さて、スペースシャトル打上げの際には、宇宙飛行士に最大3G?4Gの加速度がかかると言われています。
この加速度に打ち勝つ為に長期間にわたる訓練が為される訳ですね。

スペースシャトルに匹敵するほどの加速度を体験できる場所といえば、ジェットコースターが思い浮かびます。
日本で一番の加速度を誇るジェットコースターはどこかを調べてみました。

⇒参考サイト：ジェットコースター徹底比較

それによると、実に5Gを超えるものが2つもありました。
ヴィーナス（スペースワールド）が 5.26G、新滑空水上コースター・カワセミ（東武動物公園）が 5Gとなっています。

スペースシャトルよりも加速度が厳しいにも関らず、訓練もしていない普通の人が乗っても安全であるのは何故でしょうか。
そのポイントは
（１）加速度が掛かっている時間が一瞬である
（２）軌道が「人に優しい」曲線となっている

の二点だと思います。

このうち、後者の「人に優しい」曲線について考えてみます。
身近な例として道路の曲線をとりあげます。

車に乗っている人が如何に快適に、安全に走行できるかということは、道路設計の一番の命題になるのですが、具体的な条件を列記すると

（１）速度が速くなったり遅くなったりせず一定の速度を保つ
（２）カーブを曲がるときには急なハンドル操作を避ける
（３）人体に作用する加速度の変化をなるべく少なくする

といったところでしょうか。

車が一定のスピードで走っている時に、ハンドルを一定の角速度で切ることにより描かれる曲線が上記条件に合致しそうだ、ということが体感的に分かります。
そのような曲線だと、ハンドル操作が自然に行われ、加速度の変化が緩やかであり、人体に作用する加速度Gの変化も少なくなります。

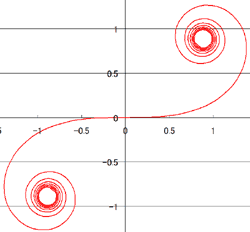
この条件により描かれる曲線をクロソイド曲線といいます。

　x座標値　x(l) ＝ a∫cos(θ²/2)dθ
　y座標値　y(l) ＝ a∫sin(θ²/2)dθ
　　　　
　積分区間[0:l]
　l：曲線上の距離

⇒クロソイド曲線をエクセルで描いてみました

基本的に、道路を設計する際にはクロソイド曲線が用いられています。

なお、クロソイド曲線が日本で最初に道路設計に導入された場所は国道17号線三国峠であり、峠には「クロソイド曲線記念碑」も建立されています。

---

日本初のクロソイド曲線を利用した道路線形の導入（一般国道17号・三国峠）

危険な山道であった三国峠。道が細く急なこの峠では、かつて多くの人々が命を落とす悲劇が絶えませんでした。
昭和27年、この山岳道路が一般国道に指定された後、改良工事が行われ、この時日本で初めてクロソイド曲線が導入されました。
これは道路の直線と力ーブの間に緩和曲線を挟み込む線形で、直線からカーブに入った場合に車に加わる加速度を押さえ、 道路から車が飛び出すのを防ぐ効果があります。 三国峠から導入されたクロソイド曲線は、その後の道路整備でも積極的に取り入れられ、各地で人々の安全を守り続けています。
自動車が走行しながらハンドルを回したときの軌跡がクロソイド曲線になることから、安全で走りやすい道路に非常に適しています。その他では道路だけでなくジェットコースターなどにも適用されています。
（出典：高崎河川国道事務所）

---

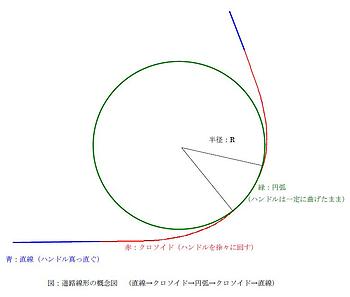
道路設計において、曲線を描く場合には、このようにクロソイド曲線を用いるわけですが、基本的に下図のように設計します。

こうすることにより、カーブに差し掛かってハンドルを徐々に一定の速さで回し始め、カーブのピークではハンドルを固定、そしてハンドルを徐々に戻し、最後は真っ直ぐに・・・という操作でスムーズにカーブを曲がることができます。

一昔前は、この曲線を描くために特殊な定規を使っていました。
これがベラボウに高価なのです。⇒クロソイド定規

今では電子計算機の発達により比較的手軽に計算できるようになりました。
便利になったものです。

彼岸明けには高速道路料金が値下げになり、ドライブを楽しむ方も多いと思います。
道路には、直線で設置できるような箇所でも、敢えて適度に曲線を加えることによりドライバーの眠気を防いだり心地よいリズム感を与えたり設計者の工夫を感じられる箇所もあります。

カーブを運転する際には設計者がどのような思いを込めて線を引いているのかを楽んでみては如何でしょうか。
　

以上は道路設計における曲線を考えましたが、これに限らず様々なことに応用できるのがクロソイド曲線です。

私たちを取り巻く「環境」はさまざまな場面で変化します。
AとBの2つの状態間を緩衝的に結ぶか結ばないかは、冒頭のスペースシャトル打上げとジェットコースターとの差にも如実に表れています。

寒い室外から暖かい部屋の中に入った時（温度の変化）、部屋の照明を点けるとき（照度の変化）などなど、このように2点間の状態を急激に遷移させるのではなく、始めは緩やかに、徐々に変化の度合いを高めていくというように工夫することが私たちにとって「優しい」ということになるでしょう。

■補記
クロソイド曲線は、「一定の速度」で走行、「一定の角速度でハンドルを回す」という条件でしたが、路面のバンク角を立体的に考慮し安定的に走行できるように設計したした曲線があります。
それはマッコーネル曲線と言われるものですが、競輪とかレースをやられている方は耳にしたことがあるのではないでしょうか。

■補記２
前に、お寺の屋根の勾配がカテナリーであることを検証しましたが、もし「雨粒たち」に優しい曲線を設計するのであれば、クロソイド曲線やマッコーネル曲線でお寺の屋根を設計してみるのもアリかもしれません。
大学の講義で、ある教授が「水路を設計するときには水の気持ちになって設計しろ」とさかんに言われていたことが強く印象に残っています。

■関連ブログ記事

お寺の屋根が美しいのには理由があります
お寺の屋根が曲線である理由・別の視点から