« 言語表現はいかにして多値論理体系で説明できるか11 | 最新記事 | 再生紙問題ー製紙業界に走る激震 »
2008年1月18日
言語表現はいかにして多値論理体系で説明できるか12

人間の目で見分けることができる色の数についてはこれまで考えてきました。
無限に限りなく近い色を系統立てて分類するために、色の三属性という性質が抽出されました。
これは「色相」「明度」「彩度」により分類を行うものであり、ルード・ハーズト・ヴント・リッジウエー・マンセルなど、諸学者に一致した分類方法であります。
(ただし、この他に材質の質感とか光沢など、色彩感覚に影響を及ぼす要素はいくつかあります)
連続した色の流れを円形に図式化したものが色環であり、この色環上の色合いを「色相」と呼びます。
この色合いを色名として区別しているわけですが、無限の色すべてに名前をつけるわけにはいきません。このために様々な分類方法が提案されているのです。
しかし、例えば色相を例にすると、分類方法によって、その細かさや範囲に差違が見られます。
表1 色相の分類方法
|
ヴント |
マンセル |
オストワルト |
日本色彩研究所 |
|
|
基本分類 |
5 |
5 |
6 |
6 |
|
中間色 |
10 |
10 |
8 |
? |
|
細分類 |
? |
40 |
24 |
23 |
色が元々光の働きかけが網膜を通して認識されるとしたら、光の波長で分類することが自然であると考えます。
表1をみると、色相として区別している数は細分類で20?40程度です。
当然、この色相に対応する名称は分類者によって異なり、また逆に同じ名前の色でも、波長の範囲は異なります。
しかし、その分類手段として、まず際立った数種類(5?6種類)の基本分類を行い、そこから中間色をおいて細かく分類していくという手法は共通しています。
色相を例にした場合、日常においては大雑把に5?6の分類、厳密に考えても20?40種類の分類があればこと足りるということを示唆しているともいえます。
このことから、色相に関しては、5ないし6値、多くてもの論理構造で日常言語の論理がなされているといって良いと考えられる。
ここで、前回までに考えた3値の真理表から発展させて、5値ないし6値と・・・・・いった多値の真理表を構築してみましょう。
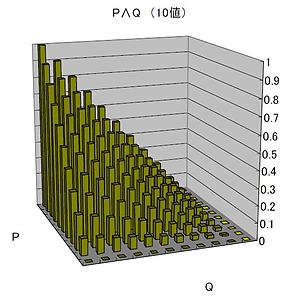
ということで、10値の真理表を作ってみました。
表2 p∧q (10値)
|
P? q |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
|
1 |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
|
0.9 |
0.9 |
0.81 |
0.72 |
0.63 |
0.54 |
0.45 |
0.36 |
0.27 |
0.18 |
0.09 |
0 |
|
0.8 |
0.8 |
0.72 |
0.64 |
0.56 |
0.48 |
0.4 |
0.32 |
0.24 |
0.16 |
0.08 |
0 |
|
0.7 |
0.7 |
0.63 |
0.56 |
0.49 |
0.42 |
0.35 |
0.28 |
0.21 |
0.14 |
0.07 |
0 |
|
0.6 |
0.6 |
0.54 |
0.48 |
0.42 |
0.36 |
0.3 |
0.24 |
0.18 |
0.12 |
0.06 |
0 |
|
0.5 |
0.5 |
0.45 |
0.4 |
0.35 |
0.3 |
0.25 |
0.2 |
0.15 |
0.1 |
0.05 |
0 |
|
0.4 |
0.4 |
0.36 |
0.32 |
0.28 |
0.24 |
0.2 |
0.16 |
0.12 |
0.08 |
0.04 |
0 |
|
0.3 |
0.3 |
0.27 |
0.24 |
0.21 |
0.18 |
0.15 |
0.12 |
0.09 |
0.06 |
0.03 |
0 |
|
0.2 |
0.2 |
0.18 |
0.16 |
0.14 |
0.12 |
0.1 |
0.08 |
0.06 |
0.04 |
0.02 |
0 |
|
0.1 |
0.1 |
0.09 |
0.08 |
0.07 |
0.06 |
0.05 |
0.04 |
0.03 |
0.02 |
0.01 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
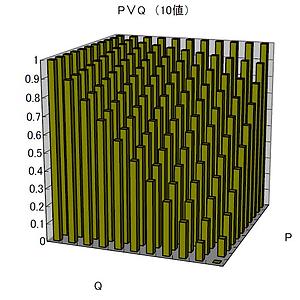
表3 p∨q(10値)
|
P? q |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
0.9 |
1 |
0.99 |
0.98 |
0.97 |
0.96 |
0.95 |
0.94 |
0.93 |
0.92 |
0.91 |
0.9 |
|
0.8 |
1 |
0.98 |
0.96 |
0.94 |
0.92 |
0.9 |
0.88 |
0.86 |
0.84 |
0.82 |
0.8 |
|
0.7 |
1 |
0.97 |
0.94 |
0.91 |
0.88 |
0.85 |
0.82 |
0.79 |
0.76 |
0.73 |
0.7 |
|
0.6 |
1 |
0.96 |
0.92 |
0.88 |
0.84 |
0.8 |
0.76 |
0.72 |
0.68 |
0.64 |
0.6 |
|
0.5 |
1 |
0.95 |
0.9 |
0.85 |
0.8 |
0.75 |
0.7 |
0.65 |
0.6 |
0.55 |
0.5 |
|
0.4 |
1 |
0.94 |
0.88 |
0.82 |
0.76 |
0.7 |
0.64 |
0.58 |
0.52 |
0.46 |
0.4 |
|
0.3 |
1 |
0.93 |
0.86 |
0.79 |
0.72 |
0.65 |
0.58 |
0.51 |
0.44 |
0.37 |
0.3 |
|
0.2 |
1 |
0.92 |
0.84 |
0.76 |
0.68 |
0.6 |
0.52 |
0.44 |
0.36 |
0.28 |
0.2 |
|
0.1 |
1 |
0.91 |
0.82 |
0.73 |
0.64 |
0.55 |
0.46 |
0.37 |
0.28 |
0.19 |
0.1 |
|
0 |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
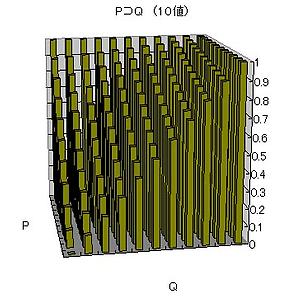
表4 p⊃q(10値)
|
P? q |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
|
1 |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
|
0.9 |
1 |
0.91 |
0.82 |
0.73 |
0.64 |
0.55 |
0.46 |
0.37 |
0.28 |
0.19 |
0.1 |
|
0.8 |
1 |
0.92 |
0.84 |
0.76 |
0.68 |
0.6 |
0.52 |
0.44 |
0.36 |
0.28 |
0.2 |
|
0.7 |
1 |
0.93 |
0.86 |
0.79 |
0.72 |
0.65 |
0.58 |
0.51 |
0.44 |
0.37 |
0.3 |
|
0.6 |
1 |
0.94 |
0.88 |
0.82 |
0.76 |
0.7 |
0.64 |
0.58 |
0.52 |
0.46 |
0.4 |
|
0.5 |
1 |
0.95 |
0.9 |
0.85 |
0.8 |
0.75 |
0.7 |
0.65 |
0.6 |
0.55 |
0.5 |
|
0.4 |
1 |
0.96 |
0.92 |
0.88 |
0.84 |
0.8 |
0.76 |
0.72 |
0.68 |
0.64 |
0.6 |
|
0.3 |
1 |
0.97 |
0.94 |
0.91 |
0.88 |
0.85 |
0.82 |
0.79 |
0.76 |
0.73 |
0.7 |
|
0.2 |
1 |
0.98 |
0.96 |
0.94 |
0.92 |
0.9 |
0.88 |
0.86 |
0.84 |
0.82 |
0.8 |
|
0.1 |
1 |
0.99 |
0.98 |
0.97 |
0.96 |
0.95 |
0.94 |
0.93 |
0.92 |
0.91 |
0.9 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
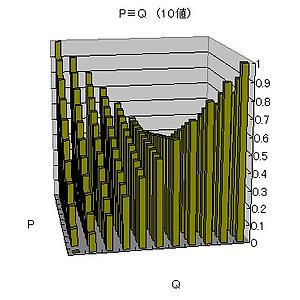
表5 p≡q(10値)
|
P? q |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
|
1 |
1 |
0.9 |
0.8 |
0.7 |
0.6 |
0.5 |
0.4 |
0.3 |
0.2 |
0.1 |
0 |
|
0.9 |
0.9 |
0.82 |
0.74 |
0.66 |
0.58 |
0.5 |
0.42 |
0.34 |
0.26 |
0.18 |
0.1 |
|
0.8 |
0.8 |
0.74 |
0.68 |
0.62 |
0.56 |
0.5 |
0.44 |
0.38 |
0.32 |
0.26 |
0.2 |
|
0.7 |
0.7 |
0.66 |
0.62 |
0.58 |
0.54 |
0.5 |
0.46 |
0.42 |
0.38 |
0.34 |
0.3 |
|
0.6 |
0.6 |
0.58 |
0.56 |
0.54 |
0.52 |
0.5 |
0.48 |
0.46 |
0.44 |
0.42 |
0.4 |
|
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
0.5 |
|
0.4 |
0.4 |
0.42 |
0.44 |
0.46 |
0.48 |
0.5 |
0.52 |
0.54 |
0.56 |
0.58 |
0.6 |
|
0.3 |
0.3 |
0.34 |
0.38 |
0.42 |
0.46 |
0.5 |
0.54 |
0.58 |
0.62 |
0.66 |
0.7 |
|
0.2 |
0.2 |
0.26 |
0.32 |
0.38 |
0.44 |
0.5 |
0.56 |
0.62 |
0.68 |
0.74 |
0.8 |
|
0.1 |
0.1 |
0.18 |
0.26 |
0.34 |
0.42 |
0.5 |
0.58 |
0.66 |
0.74 |
0.82 |
0.9 |
|
0 |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
ここに、内包と言語表現との結びつき、言語表現の内包に影響を与え、結果として異なった外延として認識される図式を導き出すこともできます。


色彩を選ぶ時、パレットの上で作る時、台布やバック紙の重ねた色や質感でそこに似つかわしい色を探します。
これはめざす表現したい事柄を自分の内なるものに克明に忠実に再現する作業には大切。
しかし布を織り、染色してまでして作ったとしても其れはいつもうまく成功するわけではないです。とくに私のよーな未熟者では・・・
そこで登場するのがデフォルメや発想の転換だと考えます。
絵画のような平面構成では色を作りタッチを変えるのは素材をMIXすることを入れても膨大な表現が可能ですが、パッチワークとの決定的な差は「素材はあくまで布であり、ロットは限られ、使える面積は多くの場合限りがある」という点に絞られ縛られることも多い事です。
昔、残ったはぎれや着られなくなった洋服など限られた範囲でしか使えない中、試行錯誤されて作られてきたゆえのいわゆる
知恵・技が鍛えられ今日に至るようです。
このように生活の中から生まれ色彩も時々の流行色を反映しながらも昔の木綿をヴィンテージとして懐古主義にひたりながらその柄や色彩の違いを楽しむ・・そして作品に反映させるという高度なアートとしての位置づけになりつつあるこのキルトという表現方法を興味深く見つめている自分がいます。。。。
どこまでも進化を続けていくアート。
パッチワークキルトがどこまでアートとして認められるのか、という事に関してはかなり論争が繰り広げられているようです。
しかしあくまで私は私らしいものを作って行こうと思います。
だってそれがわたしの、スタンダードだから。
投稿者 ゆが | 2008年1月18日 19:52
ゆがさん
パッチワークにしても点描にしても、限られた色数、面積の中で描いていくのですが、そこには制限を越えた豊かな情景が浮かび上がっていきます。
バッチワークキルトも充分アートとしての分野を確立していると思いますよ、これから楽しみにしています
投稿者 kameno | 2008年1月20日 10:07