« 仏法を伝える為に出来ること | 最新記事 | うこぎ粥 »
2010年5月 5日
国際郵便用梱包材の規格化を

海外にまとまった荷物を送る場合、その送るものによって送付方法を変える必要があります。
日数に余裕が取れる場合には船便を選ぶのが最もリーズナブルで、次いでSAL便と続きます。
発送の際に注意するべきは、包装時のサイズ、重量制限です。
特にアメリカ合衆国に送る場合は制限が厳しいので注意が必要です。
大抵の国は国際小包郵便物の制限として長さ1.5m 長さと横周の合計3m、重量 30kgと定められていますが、アメリカ合衆国は「大きさ: 長さ1.05m 長さと横周の合計2m、重量 30kg」と、梱包サイズがかなり厳しくなっています。
この「横周」というのがネックです。
縦、横、奥行きの三辺の合計ではなく、縦×2+横×2+奥行きで計算しなければなりません。
それでは、長さ1.05m 長さと横周の合計2mで、出来る限りたくさんの衣類を送りたいという場合、どのようなダンボールを用意すれば一番容量が大きくなるかを計算してみました。
(途中経過は省略します。興味ある方は最下行の More...をクリックください)
結果、縦33.3cm、横33.3cm、奥行66.8cm のダンボールに梱包することにより、最大容積の荷物を送ることが出来そうです。
(この大きさのダンボールに衣類を積めても30kgを超えませんでした)
このサイズのダンボールは、残念ながら規格化がされていないこともあり、一般には売られていません。
ゆうパック包装用品 タイプ一覧でも、一番大きなサイズ「特大」は35×45×35cmであり、もう一回り大きな箱が欲しい所です。
様々なサイズの梱包材をまとめたサイト、送料の虎を見ても縦33.3cm、横33.3cm、奥行66.8cm というサイズは掲載されていません。
特注か自分で作らなければならないのです。
生活用品を海外に送る場合など、国際小包郵便物上限サイズのダンボールは結構需要があるのではないかと思います。規格化して販売していただけたら便利なのですが。
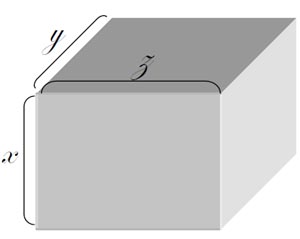
<計算メモ・アメリカ合衆国にSAL、船便で送ることができる最大容量の荷物サイズ>
条件: 2x + 2y + z ≦ 200 として
容積 V=x * y * z が最大となる x ,y ,z を求める。
まず、変数を減らすためにzを固定したときに最大となるx,y を求めることは、周囲の長さaが一定で面積Aが最大となるx,yを求めればよいから
a=2x+2y
A=xy =a/2x-x^2
Aが最大となるxを求めるために微分して
A'=a/2-2x
よって x=y=a/4の正方形の時に断面積Aは最大となる。
x=y だから
容積 Vは
V=x * y * z = x * x * z
2x + 2x + z = 200 より
z=200-4x
V=x^2 *(200-4x)
V'=400x - 12x^2
x=0 または X=100/3 (cm) の時に容積Vが最大となる。


ゆうパック包装用品 タイプ一覧でも、一番大きなサイズ「特大」は35×45×35cmであり、もう一回り大きな箱が欲しい所です。 (私ももっと大きな箱欲しいです。)
縦33.3cm、横33.3cm、奥行66.8cm のダンボール最大容積の荷物を送ることが出来そうです。 (すごいの計算ですね。)
様々なサイズの梱包材をまとめたサイト、送料の虎を見ても縦33.3cm、横33.3cm、奥行66.8cm というサイズは掲載されていません。 (でも一番いい箱はこちら!!見つけた!)
http://www.jluggage.com/packing_e.html
DC-K-8W (505 x 460 x 340) ¥550
横周の合計=1.95m!!
投稿者 匿名 | 2011年5月26日 13:09
匿名さま
規定寸法ぎりぎりに作られた箱もあるのですね。
ただ、断面が正方形の方が内容積が大きくなるので、是非容積が最大になる箱を規格化してもらいたいものです。
投稿者 kameno | 2011年5月27日 01:21
| 2011年5月27日 01:21