Teishoin's Digital Photo Log

寺社の屋根は、なぜ曲線なのかということについて、先日の お寺の屋根が美しいのには理由があります という記事で考えてきました。
今日は、それを一歩進めて、別の視点から、なぜ曲線なのかという理由について考察してみます。

話は、一旦飛躍しますけれど、今から300年以上前の1696年、ヨハン・ベルヌーイ（一世）が、自分が解くことが出来た数学の難問を、「挑戦状」として世界中の数学者に送りつけた問題をご紹介します。

その問題とは、

「高低差のある二点を通る斜面を作り、そこに玉を転がしたとすると、どのような斜面の時に一番早く二点間を転がり落ちるか」

という問題です。

二点間を結ぶ線は無限通りの方法が考えられます。
ただし、玉が自然落下していくのですから、最高点の高度が出発点よりも低い位置にある連続線でなければなりません。
思いつく条件はこれくらい。
問題文は実に簡潔です。
けれども、その答えをどう導くか・・・
ちょっと数学をかじった程度では歯が立たない問題です。
難問とは、得てしてこういうものです。

さて、ヨハン・ベルヌーイは、何故挑戦状を数学者たちに送ったのでしょうか。
そこには、当時数学の論争をしていたライプニッツとニュートン、そのライプニッツ側に立って応援していたヨハン・ベルヌーイが、ライバル・ニュートンの鼻をあかしてやろうという意図があったのです。

世界中の数学者に向けた挑戦状でしたが、期限内にその問題を解くことができたのは・・・・ニュートン、ライプニッツ、ヤコブ・ベルヌーイ、ロピタルだけでした。
とりわけ、ニュートンは当時勤務していた造幣局の激務の中、独自の解法により僅か一晩で解いてしまいます。
しかもニュートンは無記名で解答を送り返し、ヨハン・ベルヌーイはその無記名の解答を見るや、その解法からニュートンからの答案であるということを覚り、とても悔しがったというエピソードがあります。

ニュートン、かっこ良過ぎです。

・・・・この問題を解くには、斜面の関数を f (x) で表し、玉がどれだけの時間を掛けて転がるのかを求める訳ですが、単にポテンシャルエネルギーから落下速度を求めるだけでは駄目で、変分法を用いなければなりません。

詳しい解法は長くなるので割愛しますが、興味のある方は　数学のいずみ　さんのサイトをご参照下さい。

さて、得られる解（一例）は

x = - sin u + u
y = cos u - 1

となります。
これは、サイクロイドの一種で、具体的には、円を直線上に滑らずに回転させたとき、円周上の一点が描く曲線の軌跡です。（uは媒介変数）

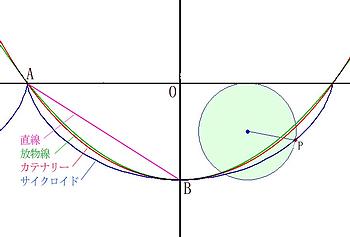
わかりやすくするために簡単な図を作成してみました。

直線（ＡＯを延長した直線）の上を薄緑色の円が回転するとします。
その円の円周上の点Ｐは、青い曲線の軌跡を描いていきますね。
この青い線がサイクロイドです。

ここで、冒頭のヨハン・ベルヌーイの問題は、図中のＡＢ間を結ぶ無数の斜面のうち、ＡＢ間を最も早く転がり落ちるのはどのような斜面かという問題でした。
図では、ＡＯの長さは円周の1/2、ＯＢの長さは円の直径となっているのでＡＢ間の平均勾配は定まってしまいますが、Ｘ軸Ｙ軸を適宜変倍することにより平均勾配は幾らでも変えることが出来ます。
参考として、ＡＢ間を結ぶ直線をピンク、放物線を緑、カテナリーを赤、サイクロイドを青で描いて図中で重ねました。

このうちの、どの斜面を転がした場合に一番早くＡＢ間を通過するのか・・・・
答えは、先の解答のとおり、青のサイクロイドなのです。

さて、前置きが長くなりましたが、ここで本題に戻ります。

屋根の果たす一番の役割って何でしょうか。
それは、雨を凌ぐこと。

すなわち、降った雨水を可及的速やかに排除することが、屋根には求められるわけです。
ということは、屋根の勾配は、雨水排除の目的からすれば、サイクロイドにするのが最適であるというわけです。

先日のトピックスでは、寺社の屋根はカテナリーになっていることが多いということを書きました。
ここで、屋根を設計・施工するという観点でカテナリーとサイクロイドを比較してみます。

力学的安定度はカテナリーが有利
雨水排除の面からはサイクロイドが有利
設計のしやすさでは紐などで簡単に曲線を描けるカテナリーが有利
施工のしやすさでは頂付近の勾配が緩いカテナリーが有利

あとは美的感覚の問題もあろうかと思いますが、寺社の屋根が古来からカテナリーが多く使われてきたというのは、上記のようなさまざまな条件による結果なのだと考えています。
それに、下に凸の曲線屋根の方が直線屋根よりも雨水が早く落下することは経験上わかっていたとしても、その最適解がサイクロイドであるということは、ニュートンの時代以前の日本では理解していなかったと思われます。
ということで、私の結論としては寺社の屋根はサイクロイドではなく、カテナリーということになります。

また、一般家庭の屋根には直線屋根が多いというのは、屋根の面積がそれほど大きくなく、雨水排除時間にさほど差異は発生しないため、むしろコストを重視して直線を採用しているのでしょう。

なお、一昔前はサイクロイドでの設計は曲線出しが困難でしたが、コンピュータの発達した現代では問題にはなりません。
サイクロイドが美的感覚としてしっくりくるのであれば、サイクロイド屋根を寺社の屋根として積極的に取り入れるのも一案かもしれません。

※でも、よく考えたら、屋根頂上付近で勾配がきつくなる為、やはり施工性に劣るという欠点。これが一番のネックなのかも。

追記：
サイクロイドには、いろいろと面白い性質があります。
その一つが、「サイクロイドのもつ等時性」というものです。

サイクロイド曲線の屋根があるとします。
その屋根に降った雨粒は、たとえ屋根の頂上付近に降った雨粒だとしても、真ん中あたりに降った雨粒だとしても、軒先付近に降った雨粒だとしても、同時刻に降った雨は、屋根を滑り落ちて同時刻に軒先に達するというものです。
ちょっと不思議な性質ですが、その証明も　数学のいずみ　さんのサイト、問題２に掲載されておりますので、興味のある方は併せてご参照下さい。